Modeling Student Knowledge
I’m enrolled in the Stanford course Probabilistic Graphical Models offered by Coursera and found a very interesting scenario concerning ways to determine and model the intelligence of a student.
Isolated Case
The first step in modeling student knowledge is to capture the information. One simple case is to look at the student’s final grade in a few classes. Suppose one student did well in the first and third course and poor in the second.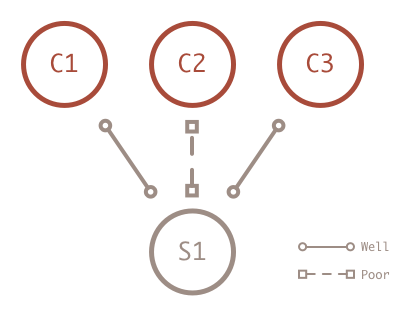
I could choose to model the intelligence of this student by first claiming that the typical student will have an 80% chance of having high intelligence. When I observe a student performing well in the first class, I can bump up his probability of having high intelligence a little, let’s say to 90%. If I observe poor performance in the second class, I can bump the probability down a little to 85%. So after two classes the student has an 85% probably of high intelligence. This isn’t the only information I have though.
Network Effect
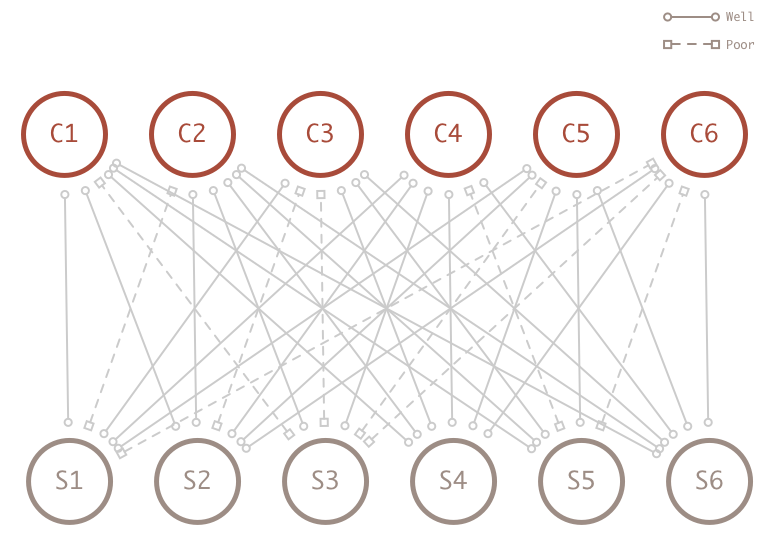When I observe all student in all classes, I suddenly have access to a lot more information the help determine the intelligence of the student in my model. Specifically I have additional information about the course the student did poor in.
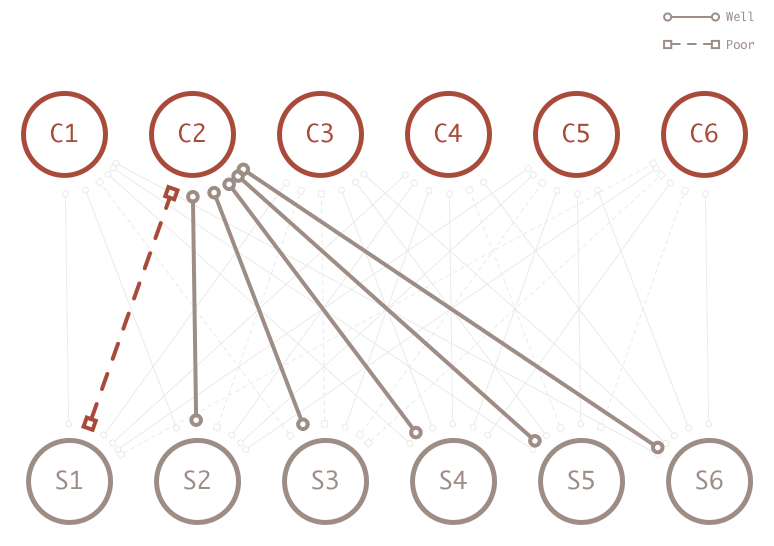Looking at the entire network, I have additional evidence that shows course 2 is a very easy course because all the other students did well. What does this additional information really give me though?
Local vs Global Scope
When I look only at the student, I have to choose a single method to increase or degrease intelligence. The simple model treats all courses the same. However, with the feedback from the network, the additional data let’s me know if some courses are more difficult than others. Now I can create a conditional probability distribution table based on the additional information.
In other words, I can enrich my model when I decide to reduce the value of intelligence. When I see a student does poorly in an easy class I bump the probability value down from 90% to 70%.
